(Registro de la Propiedad intelectual en Barcelona: 765-996394)
PRESENTACION
En contra de lo que se dice en el
libro de A. Einstein titulado: “Sobre la teoría de la relatividad especial y
general” (Ediciones Altaya S.A. 1999), en donde se afirma que la velocidad de
la luz (c) no se puede sobrepasar, nosotros hacemos un planteamiento matemático
para demostrar que una partícula sí que puede sobrepasar esta velocidad.
Cuando transcribamos algún contenido
del libro que tomamos como referencia, lo escribiremos entre comillas y con
letra de cursiva.
1.- ¿DONDE APARECE QUE LA VELOCIDAD
DE LA LUZ NO SE PUEDE SOBREPASAR?
En la página 36 del libro que tomamos
como referencia, después de hacer una aplicación de la formula del espacio de
las Transformaciones de Lorentz, aparece la siguiente sentencia:
“Para velocidad v =c sería
y para velocidades aún mayores la raíz se haría imaginaria. De aquí inferimos que en la teoría de la relatividad la velocidad (c) desempeña el papel de una velocidad limite que no puede alcanzar ni sobrepasar ningún cuerpo real. Añadimos que este papel de la velocidad (c) como velocidad limite se sigue de las propias ecuaciones de la Transformación de Lorentz porque estas pierden todo sentido cuando (v) se elige mayor que (c). “
El que una ecuación “pierda todo el
sentido” para unos valores de sus variables, quizás esta frase ya nos indique
que no está eligiendo el camino adecuado para valorar lo que pretende. Si está
ecuación fuese adecuada creemos que, refiriéndose a las variables que la
componen, tendría que definir para que valores pierde su campo de validez. No
debe ser la ecuación que “pierda su sentido “sino que debemos definir
cuando sus variables pierden su campo de validez.
¡Claro que estas ecuaciones pierden
todo sentido cuando (v) es mayor que (c) ya que no sirven precisamente para el
cometido que quiere darle!… En este caso el observador no tiene campo de visión
del Evento que se quiere observar. Pero no tiene nada que ver que el evento no
exista y se mueva a cualquier velocidad.
Debemos elegir el planteamiento
matemático adecuado para que entre la comparación de la velocidad´(v) de un
cuerpo móvil y la velocidad de la luz (c) no se produzca esta incompatibilidad.
Esto es lo que vamos a estudiar.
2.- PLANTEAMIENTO GEOMETRICO EN LA
OBSERVACION DE UN EVENTO QUE OCURRE EN EL ESPACIO SIDERAL
En el estudio de la visión de la
aparición de un Evento que ocurre en el espacio sideral, observado desde un Sistema
de Referencia Móvil, procederemos de la siguiente forma:
Situamos tres puntos en el espacio
sideral. Un punto (E) se identificará como el lugar en que ha aparecido o
nacido el Evento. Otro punto (F) representará el final de la duración del
Evento. Lo identificaremos como el final de su EXTENSIÓN. Un tercer punto (PO) será el punto de
observación del Evento. Para realizar los cálculos, estos tres puntos estarán
distribuidos de tal forma que formen un triángulo rectángulo.
La figura representa que la situación en donde nace el evento es fija (SRF). El punto de observación (PO) es móvil (SRM). Puede irse desplazando, claro está, considerando siempre la figura del triángulo rectángulo.
Con esta figura geométrica podemos
representar todas las variables y parámetros que intervienen en el proceso de
observación realizado desde un (SRM), de un Evento que sucede en un (SRF). Con el
auxilio de esta figura geométrica podremos hacer el planteamiento que nos
permitirá obtener la expresión matemática:
conocida como el Factor de Lorentz.
La interpretación de la anterior figura es la
siguiente:
Queremos
observar desde un punto móvil (PO), la Extensión del Evento. Esta Extensión
queda representada en el dibujo mediante: c.(tp), siendo (c) la velocidad de la
luz y (tp) al que le llamaremos Tiempo Propio del Evento. El punto
(PO) por ser móvil lo incluimos dentro de un Sistema de Referencia Móvil (SRM).
La variable
(td) representa el Tiempo de Desplazamiento de un observador para
situarse en el punto de observación (PO), habiendo partido del punto (F). Este
punto (F) lo identificamos para señalar el final del: c.(tp). Consideramos
este punto (F) como el punto de partida del desplazamiento, ya que tenemos que
asegurar que cuando se llegue al punto de observación (PO) ya se ha
desarrollado toda la Extensión del Evento. (Observe el lector que es una
condición geométrica que estamos imponiendo). La variable (tr) significa el
tiempo de recorrido. Por lo que: c.(tr) es el espacio que existe
entre el punto (E) de aparición del Evento y su punto de observación. Es el
recorrido de la imagen. Es necesario que
desde el punto (PO) haya llegado la información de la aparición del Evento.
Estas serán
las “reglas de juego” que rigen en la observación de un Evento que se produce
en un determinado lugar del espacio sideral y que un observador móvil
(movimientos relativos) observa su aparición y duración.
3.-CONDICIONES DE VISION DE UN EVENTO
Y ENFOQUES MATEMATICOS PARA CUMPLIR ESTA CONDICION
Para poder
observar un Evento, que se produce en un determinado punto (E) del espacio
sideral, desde un punto de observación móvil (PO), dos CONDICIONES DE VISION DEL
EVENTO, serán:
Que el
observador ya esté situado en el punto de observación (PO) y que la imagen del
Evento haya llegado también a este punto.
Podemos
elegir dos enfoques matemáticos diferentes para cumplir las Condiciones de Visión
del Evento.
CONDICION DE
SINCRONIZACION.
Esta
condición exige que el tiempo de recorrido (tr) de la Ia imagen del
Evento, desde el punto (E) al punto (PO), sea igual al tiempo de desplazamiento
del observador (td), desde el punto (F) al punto (PO). O sea (tr)
= (td)
PLANTEAMIENTO
DE COMPENSACION EN LOS RECORRIDOS
Otro enfoque
matemático que podemos dar para cumplir las Condiciones de Visión del Evento lo
llamaremos: “Planteamiento de Compensación en los Recorridos”.
Supondremos
que, para que la visión del Evento y la llegada del observador lleguen juntos en
el mismo punto de observación (PO) , si la velocidad (v) de desplazamiento del
observador es superior a la velocidad de la luz (c) en el recorrido que realiza la luz (la imagen
del Evento), entonces también supondremos que su tiempo de desplazamiento (td)
es menor que el tiempo de recorrido (tr) de la imagen del Evento.
O sea: Si (v) > (c) implica que (td)
< (tr)
Al
plantearse la realización del cálculo matemático necesario para obtener la
formula que nos permite valorar el Tiempo Propio (tp) de un Evento, nos
olvidaremos de la condición de Sincronización y consideraremos la posibilidad
de que puedan compensarse una mayor velocidad (v) con un menor Tiempo de
Desplazamiento (td)
Este planteamiento
hará que la fórmula final que nos permita valorar el (tp), tenga
diferente estructura de la que se obtendria al aplicar la condición de Sincronización
y con esto “no pierda el sentido” como dice A. Einstein en su libro.
4.- DOS SUCESOS INCOMPATIBLES EN
MATEMATICAS
Podemos
elegir dos caminos (dos modelos matemáticos) para visualizar y poder
cuantificar el valor del (tp). Pero, aunque los dos permiten obtener
el valor del (tp), uno de ellos está limitado y produce una
incompatibilidad matemática según que valores se asignen a su variable (v).
Partiendo
del triángulo rectángulo que nos sirve como patrón matemático, decimos lo
siguiente:
Si
imponemos: (tr) = (td) (una condición)
Y
suponemos
(v) > (c) (otra condición)
esta suposición
produce un suceso incompatible en matemáticas
ya que entonces
implica que: (td). (v) > (tr). (c)
y
en un triángulo rectángulo, es incompatible
que un cateto sea mayor que su hipotenusa.
Este camino
incompatible matemáticamente, es el que eligió el autor del mencionado libro
para justificar la invalidez del factor de Lorentz cuando (v) es igual a (c)
No obstante,
en un posterior ensayo veremos que el camino de considerar la condición de Sincronización
nos conduce a darnos un resultado que nos será útil para iniciar otro análisis.
Es por estos que en el siguiente párrafo explicamos su desarrollo matemático.
4.- DESARROLLO MATEMATICO PARA LA
OBTENCION DEL TIEMPO PROPIO (TP) DE UN EVENTO, APLICANDO LA
CONDICION DE SINCRONIZACION
Para hacer los cálculos para obtener la visualización y el
valor del (tp) desde el punto de observación del Evento (PO), vamos a
imponer la condición de SINCRONIZACION Se trata de que el observador del Evento
haya llegado a tiempo a observarlo “entero” por lo que debe partir del punto
(F) en el que ya puede verse toda la extensión del Evento. Además, otra condición es que llegue en el
punto (PO) precisamente cuando haya llegado la imagen del Evento. Por lo que,
al iniciarse el proceso de cálculo, impondremos la condición:
(td)
= (tr)
y se
sustituye el valor (tr) por su equivalente (td).
Para iniciar el estudio matemático observaremos la
figura que hemos dibujado en el párrafo 2, y procederemos a desarrollar los
cálculos, aplicando el Teorema de Pitágoras.
Exigiendo el cumplimiento
de la Condición de Sincronización:
(td)
= (tr)
nos permite hacer la sustitución de (tr)
por (td) con lo que se obtiene:
Agrupando términos se tiene:
Y de aquí obtenemos:
En la anterior formula, a
la expresión:
se la conoce como Factor de Lorentz Recordemos que este
planteamiento es el que produce un suceso
incompatible en matemáticas pero precisamente es el que aceptó A. Einstein y
sus seguidores.
5.- DESARROLLO MATEMATICO PARA
OBTENER EL (Tp) UTILIZANDO EL PLANTEAMIENTO DE COMPENSACION EN LOS RECORRIDOS
Podemos dar
otro enfoque para valorar el Tiempo Propio (tp) de un Evento (E),
que se produce en un Sistema de Referencia Fijo (SRF), desde otro Sistema de Referencia
Móvil (SRM).
En este otro
enfoque las CONDICIONES DE VISION DEL
EVENTO la haremos cumplir de
otra forma diferente de como la hemos expuesto en el anterior párrafo.
Utilizaremos el Planteamiento de Compensación
en los Recorridos.
Recordemos
que este planteamiento implica que un mayor valor de la variable (v) implica un
menor valor de la variable (td) es decir, justificaremos lo
siguiente:
Si v > c implica
que (td) < (tr)
Con esta
justificación y NO teniendo en cuenta la igualdad
(tr)
= (td) que habíamos comentado en el anterior caso, procedemos a
desarrollar el camino para obtener el valor del Tiempo Propio (tp)
del Evento y con ello su Extensión (c. (tp)).
Utilizaremos
como pauta de observación la figura que hemos dibujado en el párrafo 2. Los
pasos a seguir son los siguientes:
Con lo que hemos obtenido el Tiempo Propio del Evento.
Nos preguntamos: ¿es válida
esta expresión matemática obtenida? Si es valida podremos aceptar que UNA PARTÍCULA VIAJANDO EN DIRECCIÓN DEL EJE
(X) DEL REFERIDO DIBUJO, PODRÁ ALCANZAR UNA VELOCIDAD: (V) > (C).
Debemos estudiar el
campo de validez de la anterior fórmula.
6.- CAMPO DE VALIDEZ DE LA RESPUESTA
OBTENIDA UTILIZANDO EL PLANTEAMIENTO DE COMPENSACION EN LOS RECORRIDOS
Analizaremos
el campo de validez de la fórmula:
que hemos obtenido en el anterior párrafo.
Observamos si se cumple la condición:
Valdría cero cuando:
También sería válida la fórmula cuando (v) fuese mucho mas
pequeña que (c), o sea: v<<<c. Entonces ocurriría que, muy
aproximadamente, tp = tr
Lo que indicaría que estábamos en el punto de partida (F) en el
que el recorrido de la imagen de la luz es igual a la Extensión del Evento.
(NOTA: Profundizando algo
más en el tema de la validez de la fórmula que hemos obtenido, podríamos
preguntarnos qué ocurriría si considerásemos velocidades (v) muy superiores a
la de la luz. O sea, si (v)>>>(c). Esto haría variar los valores del triángulo
rectángulo en que se apoya el planteamiento de la formula, obteniendo un
desplazamiento sobre el cateto base muy pequeño y un Tiempo Propio (tp)
muy grande, por lo que la Extensión: c.(tp) del evento sería muy
grande.
Dese cuenta que ahora no estamos valorando exclusivamente el
valor:
si no sus recorridos a través de su tiempo. ¿Quizás este es el comportamiento de las partículas?... Dejamos está cuestión para que la juzguen los expertos en micropartículas)
(NOTA: En el librito “Teoría de la relatividad.- Critica de un
disparate analizado en siete fascículos” encontrará siete temas de debate sobre
esta teoría).











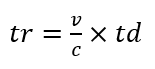


No hay comentarios:
Publicar un comentario