(Registro de la Propiedad Intelectual B-1221-21)
PRESENTACION
En nuestro libro
titulado; “Teoría de la relatividad. Crítica de un disparate analizado en siete
fascículos”, nos dedicamos a criticar las diferentes falacias que aparecen
escritas en la Teoría de la Relatividad. Ahora, nos dedicaremos a investigar
algunos aspectos de esta Teoría que posiblemente queden algo oscuros. Con esta
introducción queremos hacer diferenciar lo que fue una crítica a unos
postulados, de lo que ahora se trata. Se trata de un trabajo de investigación
del mismo autor de la citada crítica.
En
uno de los fascículos del mencionado libro citábamos “el enigmático Factor de
Lorentz”, indicando con esta expresión su contribución a la falacia de la
“dilatación del tiempo” sin apoyarse en ningún criterio lógico. Tengamos en
cuenta que, según cuenta la historia, estas expresiones matemáticas se obtuvieron
empíricamente. Ahora haremos la
“anatomía” a este Factor para indagar la función matemática que cumple. Al
final demostraremos que las Fórmulas de Transformación de Lorentz demuestran
que se produce un ALARGAMIENTO del tiempo de visión de las variables Espacio y
Tiempo de un fenómeno físico, y descartaremos la falacia de la DILATACION DEL
TIEMPO.
UNA
DE LAS APARICIONES DEL FACTOR DE LORENTZ
En la Teoría de la Relatividad, una de sus partes en que interviene el
Factor de Lorentz es en las Fórmulas de Transformación. Recordemos que la
expresión de este factor
Nos dedicaremos a estudiar la función que cumple esta expresión matemática,
pero antes comentaremos algo sobre las conocidas Formulas de Transformación de
Lorentz
Para introducirnos en el tema de las fórmulas de las Transformaciones de
Lorentz, citamos lo siguiente.
En el libro “Sobre la teoría de la relatividad especial y general” de A.
Einstein, en su página 32 (Edición “Alianza Editorial”), describe la forma y
utilidad de las fórmulas llamadas de las Transformaciones de Lorentz, de la
siguiente manera:
“Dadas las cantidades (x,y,z,t)
de un suceso respecto a (k), ¿Cuáles son los valores (x`,y`,z´,t´) del mismo
suceso respecto a (k´)?
Las relaciones hay que elegirlas
de tal modo que satisfagan las leyes de propagación de la luz en el vacío para
uno y el mismo rayo de luz (y además para cualquier rayo de luz) respecto a (K)
y (K´).”
Y prosigue diciendo:
“El problema queda resuelto por las
ecuaciones”
Fórmula del
Espacio
Figura 1
Fórmula del Tiempo
Figura 2
Y, en esta misma página del citado libro, se dibuja el siguiente sistema de coordenadas (k) y (K).
Figura 3
La variable (v) significa la velocidad relativa que tiene el sistema (K´) con respecto al sistema (K).
La explicación que aparece en el citado libro, junto con el anterior
dibujo, poco ayudan a comprender la finalidad y forma de utilizar las citadas
formulas.
Puede confundirse la designación del eje de coordenadas (X) con el valor de
la variable (x) a transformar. Utiliza tres ejes coordenados cuando, tal como
veremos más adelante, solo harán falta dos ejes de coordenadas. Debido a esta
dificultad de interpretación, hemos optado por crear nuestro propio diseño para
analizar la estructura matemática de las Fórmulas de las Transformaciones de
Lorentz.
ANALISIS DE LA VISION DEL FENOMENO DE LA TRANSFORMACION DE LAS VARIABLES DE
UN SUCESO.
En primer lugar, presentamos unas definiciones que utilizaremos en nuestro
estudio.
Al fenómeno físico que queremos observar le llamaremos EVENTO y lo
representaremos por (E).
Utilizaremos unas coordenadas cartesianas (X, Y) para situar el (E) en el
espacio sideral. Debemos considerar que estamos tratando con MMOVIMIENTOS
RELATIVOS, por lo que debemos considerar un Sistema de Referencia Fijo (SRF) y
un Sistema de Referencia Móvil (SRM) respecto a este (SRF).
A la duración o amplitud de las variables Espacio (e) y Tiempo (t)
correspondientes al (E) le llamaremos EXTENSIONES.
La magnitud de las Extensiones la llamaremos Tiempo Propio y la
representaremos con la variable (tp).
En cuanto a la visión del fenómeno físico decimos lo siguiente:
En la visión del fenómeno de la transformación de las variables de un
suceso, distinguiremos dos partes.
PRIMERA PARTE
En una primera parte consideraremos el TRASLADO de los ejes coordenados y
el resultado de este traslado que afecta a las cifras de las variables Espacio
(e) y Tirmpo (t) del suceso.
En la siguiente figura el observador VISUALIZA este traslado.
Figura 4
Este observador puede valorar el nuevo valor (x´) que tenía la variable (X)
antes del traslado, de acuerdo con la expresión:
Las magnitudes del Espacio (e) y Tiempo (t) de un fenómeno físico (E) quedan registradas como su longitud en la coordenada: x. Decimos que es su Extensión (X).
Esta Extensión es la que se transforma (o traspasa) al desplazar las
coordenadas.
Estas variables (X) serán los valores de la Extensión del Evento.
Mas adelante veremos que estas expresiones de (X) las identificaremos como
el Tiempo de Desplazamiento (td) de las coordenadas, y que las
Extensiones las identificaremos con el Tiempo Propio (tp) de este
Evento.
Para realizar la valoración del resultado de la anterior expresión sería
necesario:
Situar el Evento (E) en una determinada posición del espacio sideral
determinada por las coordenadas cartesianas (K).
Conocer la distancia entre los ejes (K) y (K´) que se calcularía conociendo
la velocidad (v) y el tiempo (t) del traslado.
Observe el lector que la anterior expresión es la que aparece en el
numerador de la Formula de Transformación del Espacio y, según veremos más
adelante, también se corresponde con la Formula de Transformación del Tiempo.
SEGUNDA PARTE
En la Primera Parte hemos considerado que los ejes coordenados ya están
situados en su lugar de observación. El TRASLADO ya estaba realizado y por lo
tanto se trataba de una VISION ESTATICA. Es una fotografía de un suceso.
Vamos ahora a considerar una VISION DINAMICA. Se trata de querer observar
el valor de las Extensiones del Evento (E) mientras el eje de situación del (E)
se está moviendo. Se está trasladando. (Tengamos en cuenta que estamos tratando
con MOVIMIENTOS RELATIVOS).
Esta cuestión entra de lleno en el estudio del Factor de Lorentz que, según
podemos comprobar, aparece en el denominador de las Fórmulas de Transformación.
Utilizaremos nuevos gráficos para justificar el planteamiento de la VISION
DINAMICA del Tiempo Propio (tp) correspondiente a la Extensión de un
Evento (E).
CONDICIONES DE SINCRONIZACION DE LA VISION DE LA IMAGEN DEL EVENTO.
Iniciamos ahora la explicación de un tema que implica al denominador que presentan
las dos Fórmulas de Transformación. Veremos que en él incluiremos el Factor de
Lorentz.
Para analizar los conceptos simultáneos de MOVIMIENTO y OBSERVACION,
dibujamos la siguiente figura. Le llamaremos: esquema operativo.
Figura 5
En una determinada posición del espacio sideral está situado un fenómeno físico al que queremos cuantificar la magnitud de su variable espacio (x). Recordemos que: al fenómeno físico lo identificaremos como un EVENTO (E). La magnitud de (x) le llamaremos su EXTENSION. En este esquema operativo la Extensión la identificaremos como el Tiempo Propio (tp) de (E) y la representaremos sobre el eje (Y) del dibujo. La magnitud de la Extensión la valoramos como (c.tp), siendo (c) la velocidad de la luz y la representamos en zig-zag como si fuese un rayo.
Se trata de observar la Extensión
del (E) desde el punto (F) representado en el esquema Un observador fijo,
situado en el origen de los ejes coordenados (X, Y) podría observar toda la
amplitud (c.tp) de la Extensión espacio (e) o tiempo (t) del Evento
(E).
Para que esto mismo
ocurra desde otro punto del espacio sideral será necesario que el tiempo de DESPLAZAMIENTO
(td) que habrá tardado el observador en situarse en aquel punto, sea
igual al tiempo de recorrido (tr) de la IMAGEN de la Extensión. Es decir:
(td) = (tr)
para que el observador no
se retrase o se adelante respecto a la llegada de la información al punto de observación.
A esta igualdad le
llamaremos “Primera Condición de Sincronización” Este Tiempo de Recorrido (tr)
al igual que el (tp) lo hemos dibujado en zig-zag por recorrerse a
velocidad de la luz (c).
(NOTA: Tratándose de dos
Sistemas de Referencia Inerciales (SRI) también podríamos hacer referencia al
cálculo diferencial. Argumentaríamos que el Sistema de Referencia Móvil se
mueve de tal forma que un diferencial de tiempo de traslado
Una
segunda condición de sincronización es que el tiempo transcurrido durante el
desplazamiento (td) sea igual a la Extensión (tp) del
Evento. Es decir:
(td) = (tp)
para que el observador pueda contemplar desde el punto de observación, toda
la Extensión.
(NOTA: Podemos justificar la forma alargada de la figura 5, correspondiente
a un triángulo rectángulo, de la siguiente forma:
Si (tp) = (td)
y como c>>v => c.(tp) > v.(td)
que nos hace pensar que si
el triángulo rectángulo fuese equilátero la velocidad (v) debería ser igual a
(c) y seria otro tema de análisis).
EL FACTOR DE
LORENTZ. UNA EXPRESION MATEMATICA QUE APARECE EN LAS FORMULAS DE TRANSFORMACION
Estudiaremos la forma en
que podemos RELACIONAR el Tiempo Propio (tp) de las Extensiones, con
el Tiempo de Desplazamiento (td) al punto de observación. Para esto
observaremos la Figura 5 y procederemos a desarrollar los cálculos, aplicando
el Teorema de Pitágoras.
Exigiendo el cumplimiento de la Primera Condición de Sincronización:
(td)
= (tr)
nos permite hacer la sustitución de (tr) por (td) con lo que se obtiene:
Agrupando términos se tiene:
Podemos transformar el
denominador de la siguiente forma:
Eliminando (c), da como resultado
A
la expresión:

Nos permite relacionar el Tiempo Propio (tp) del Evento con el Tiempo de Desplazamiento (td) del observador. Junta los conceptos que habíamos hablado: Posición y Movimiento.
EL
FACTOR DE LORENZ COMO UNIDAD DE MEDIDA DEL TIEMPO PROPIO DE LAS VARIABLES ESPACIO
(e) Y TIEMPO (t)
Para
deducir como podemos cuantificar el Tiempo Propio (tp),
correspondiente a la IMAGEN de la Extensión de una variable (x) debido al
MOVIMIENTO, a partir del Tiempo de Desplazamiento (td) que han
recorrido las coordenadas (K´), hacemos el siguiente razonamiento:
Partimos
la Relación de equivalencia que habíamos encontrado:
De aquí podemos deducir otra relación de equivalencia con el Factor de Lorentz:
El
cociente:
![]()
podemos decir que es una forma de cuantificar el (td) en unidades (tp)
Por lo que el Factor de Lorentz es un factor transformador o corrector, que transforma el Tiempo de Desplazamiento (td) en unidades de Tiempo Propio (tp). Por lo que, aplicando este factor al (td) se obtiene:
De esta forma hemos justificado la existencia del Factor de Lorentz en las referidas fórmulas.
Observe que en la PRIMERA PARTE habíamos dado la expresión:
en la que justificábamos que la podíamos considerar como un Tiempo de Desplazamiento (td).
Nos falta todavía aclarar una cuestión.
Ahora
estamos hablando de un tiempo de desplazamiento (td). ¿Cómo podemos
aplicar el Factor de Lorentz en la Fórmula del Espacio, como denominador de la expresión:
para que así pueda valorarnos el (tp)?
Para
aclarar este concepto diremos que hasta ahora hemos estado hablando de
RECORRIDOS de las coordenadas (K´), y esto es lo que manifiesta la anterior
expresión, pero ahora entramos en valorar DISTANCIAS.
En
este nuevo enfoque para valorar las Distancias utilizarnos la velocidad de la
luz. Tal como veremos seguidamente estas distancias las valoraremos en unidades
velocidad de la luz (uvl).
Esta
expresión representa un tiempo de desplazamiento valorada en estas unidades.
Creemos
que ha llegado el momento de hablar de la expresión:

que
aparece en el numerador de la Formula del Tiempo.
FACTOR CORRECTOR DE LAS VELOCIDADES. MEDIDA DEL
TIEMPO DE DESPLAZAMIENTO (td).
En
la percepción de la imagen de un evento entre dos Sistemas de Referencia
Inerciales con una velocidad (v) entre ellos, debemos tener presente que
estamos utilizando dos tipos de velocidades completamente diferentes en cuanto
a naturaleza y órdenes de magnitud. Se trata de dos Magnitudes Físicas
diferentes. Podemos decir que la
velocidad relativa (v) entre el (SRM) y el (SRF) es entre masas mientras que la
velocidad de transmisión de la información corresponde a una onda electromagnética
con una velocidad de la luz (c) muy por encima o por lo menos muy diferente de
la velocidad (v). Es obvio que, aunque se trata de dos expresiones que están
relacionadas con “la rapidez”, son diferentes. No tienen la misma naturaleza
física. Deben tratarse como diferentes. La velocidad de la luz (c) es siempre
la misma. Es inherente a sí misma. Es una constante y con un orden de magnitud
infinitamente más grande que la que se supone que se da sobre el eje (X). Es
decir (v). No podemos comparar o establecer una relación entre dos longitudes o
dos tiempos que estén medidos utilizando patrones diferentes de medir las
velocidades. Deben normalizarse de tal forma que ambas utilicen el mismo tipo
de patrón.
Utilizamos
la velocidad de la luz (c) como patrón. O sea, los 300.000 kms/seg. como unidad de velocidad
Para
hacer las referidas conversiones debemos tener en cuenta los siguientes
criterios a seguir:
Todas las longitudes se cuantificarán utilizando:
“unidades velocidad luz” (uvl).
Esto quiere decir que: las (uvl) son las que se
consumirían para desplazarse entre dos determinados puntos de referencia. Por ejemplo, podemos escribir: x = k (uvl)
refiriéndonos a que una determinada longitud (x) se encuentra, o requeriría k
(uvl) para llegar a ella. (La “unidad luz” es una medida de velocidad que vale:
300.000 kms/seg. O sea, una (uvl) es igual a 300.000 kms/seg.)
Una
relación tal como: (v / c) asigna una fracción de (uvl) a una determinada velocidad
(v), ya que (c) es una cantidad fija que se toma como unidad, mientras que (v)
es la velocidad relativa entre los (SRI), valor diferente en cada caso en
concreto.
Para
cuantificar una longitud (l) aplicaremos la expresión:
l = x.(v /c)
Esta
expresión responde a la pregunta: Una longitud (x) que se ha recorrido a la
velocidad (v) ¿a qué longitud (l) equivale si la velocidad fuese la de la luz
(c)?
Para
obtener el tiempo de desplazamiento (td) de un Sistema de Referencia
Móvil (SRM) sobre el eje (X), operando con (uvl), deberemos dividir el espacio
(l) por la velocidad de la luz (c).
O
sea:
(td) = (l) / (c) y como l = x.(v /c)
se obtiene: (td) = (l)/(c) => (x).(v/c)/(c) =>
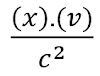
Expresión que aparece en el numerador de la Fórmula
de la Transformación del Tiempo y que se trata de la expresión de un tiempo.
CONSTANCIA
DE LA RELACION ENTRE EL (td) Y EL (tp). TEOREMA DE TALES
Para facilitar la interpretación de lo que vamos a exponer presentamos la
siguiente figura
Figura 6

El dibujo representa una determinada posición, en el espacio sideral, de las coordenadas (K´) después de haber recorrido un cierto espacio valorado como (td).
En esta situación de las coordenadas (K´) podemos aplicar, por ejemplo, la
Formula del Espacio para visualizar la Extensión de un Evento (E) situado en
las coordenadas (K).
Nos preguntamos ahora:
Si las coordenadas (K´) continúan desplazándose ¿nos valdrá la aplicación de
la Formula para todas las distintas situaciones que pueda alcanzar?
La respuesta lógica parece que debe ser afirmativa. Sin embargo, no podemos
dar esta respuesta sin dotarla de cierto rigor científico.
Para justificarlo decimos lo siguiente:
Pretendemos demostrar que el cociente:
debe ser un valor constante (K) para cualquier valor del (td).
Si demostramos que:
para cualquier punto del recorrido (td), entonces podremos admitir para todos los puntos del recorrido de las coordenadas.
La
demostración la realizamos utilizando el Teorema de Tales, cuyo cumplimiento lo
ilustramos con la siguiente figura.
Figura 7
Tal como convenimos, en el cateto vertical representaremos la extensión (tp) del Evento. Esta extensión tiene un valor determinado para un determinado fenómeno físico a observar.
Situado
el punto de observación a una determinada distancia, al determinar el valor de
la relación:
Es evidente que esta condición de conservarse los valores:
es general. Para un fenómeno en concreto vale para su valor constante (tp) y posibles valores variables de (td).ANALOGIA
DE LAS TRANSFORMACIONES DE LORENTZ CON EL EXPERIMENTO MENTAL DEL VAGON DE TREN
En
este capítulo recordaremos lo que expusimos en nuestro libro: “Teoría de la relatividad.
- Critica de un disparate analizado en diete fascículos”, respecto al
“Experimento mental del Vagón de Tren”. El propósito de este recordatorio es el
de establecer una analogía entre este experimento y las Fórmulas de Transformación
que hemos estudiado, y de aquí sacar la conclusión de que estamos frente a un ALARGAMIENTO
DE LA VISION DE UN HECHO O CAUSA. No se trata de una DILATACION DEL
TIEMPO.
Recordemos
que en el citado libro cuestionamos las conclusiones de este experimento y lo
etiquetamos como la “génesis del disparate”. Dijimos que se trataba de dos experimentos
diferentes y simultáneos. Esto nos hace dar cuenta que hemos obtenido una
RELACION entre dos magnitudes físicas procedentes de dos fenómenos diferentes.
Traspasamos
el dibujo de aquel experimento mental:
En la parte izquierda del dibujo se representa el fenómeno de la reflexión del rayo de luz en un espejo que está situado en el techo del vagón. El vagón de tren está parado y el tiempo de ida y vuelta de la reflexión en el espejo que registra el observador (O1), es realmente el Tiempo Propio (tp) del fenómeno físico.
Otro
observador (O2) situado quieto en el terraplén, tardaría un tiempo
(td) mayor que el que observa el (O1) debido a que en el
fenómeno de la reflexión de la luz contempla también el desplazamiento del
espejo.
Queda
claro que se trata de dos ensayos diferentes.
En
la explicación de las Fórmulas de Transformación hemos mencionado el Tiempo
Propio (tp) de la Extensión del Evento, que lo podemos asociar al (tp)
del fenómeno de la reflexión del rayo de luz. Esta interpretación queda
expuesta en la parte izquierda de la Figura 8. Recordemos que el (tp)
es inherente al fenómeno. En el caso del vagón de tren corresponde al fenómeno
de la reflexión de la luz en el espejo. En el caso de las Fórmulas corresponde
a la valoración del fenómeno de la VISION de la variable Extensión de un
Evento, observada en un determinado momento. Esta es la fotografía del
fenómeno. Pero además hay que tener en cuenta que la observación se hace desde
un Sistema de Referencia Móvil (SRM).
La
siguiente figura intenta demostrar nuestra afirmación
El Tiempo Propio (tp) del fenómeno físico de la reflexión del rayo de luz en el espejo queda representado en la parte izquierda del dibujo. Con el vagón parado.
En
la parte derecha del dibujo aparece un observador fuera del vagón. Está fijo en
el suelo y observando el recorrido del rayo de luz mientras el vagón se está
desplazando durante un Tiempo de Desplazamiento (td). Es evidente
que se apreciarán distinto valores de observación del fenómeno. Se obtendrá
(td)
> (tp). esta es la interpretación que debemos darle a la referida
Formula al considerar la observación desde un Sistema de Referencia Móvil
(SRM).
LAS
FORMULAS NOS INDICAN QUE SE TRATA DE: UN ALARGAMIENTO DE LA VISION DE LAS
EXTENSIONES. NO SE TRATA DE UNA DILATACION DEL TIEMPO
Auxiliándonos
con el ejemplo del experimento mental del vagón de tren, justificaremos el
ALARGAMIENTO de la VISION de las Extensiones de un Evento.
Veamos
que nos piden las Fórmulas para obtener respuestas:
Recordemos
que el Factor de Lorentz lo incorporamos a las fórmulas cuando contemplamos una
VISION DINAMICA del fenómeno a observar.
En
primer lugar, hablábamos de una VISION ESTATICA que es lo que ha ocurrido al
cambiar las referencias debido al desplazamiento de las coordenadas. Es
equivalente al Tiempo Propio (tp) del proceso, que registra el
operario que va dentro del vagan de tren.
Otro
experimento es la VISION DINAMICA que consideramos que el observador contempla
el movimiento del experimento. No se mueve con él. Ha salido del mismo. En esta circunstancia su
medida de la VISION de la duración de la Extensión del Evento será más larga
puesto que está añadiendo el tiempo que toma el proceso en desplazarse hasta el
punto de que se considere el final de la observación. Podemos ver la analogía
que estamos estableciendo con el observador que está fijo en el suelo en el
ejemplo del experimento mental del vagón de tren.
Este
incremento en el tiempo de observación se refleja en la formula al incorporar
el Factor de Lorentz.
En
primer lugar, tengamos en cuenta que:
Recordemos que la expresión del numerador de la Formula del Espacio es:
Por lo tanto, la expresión completa de la formula:indica que se ha aumentado aquel valor inicial y esto es debido a considerar el movimiento de desplazamiento que se está produciendo.





















No hay comentarios:
Publicar un comentario