PRESENTACION
Leyendo en el libro de A. Einstein
titulado: “Sobre la teoría de la relatividad especial y general “el tema de las
Fórmulas de las Transformaciones de Lorentz, nos han surgido algunas dudas.
Analizadas estas dudas, hemos visto que proceden de dos errores. Se trata de
los mismos errores que ya expusimos en anteriores de nuestros ensayos, en los
que denunciábamos que a través de los movimientos relativos el autor del citado
libro confundía el verbo VER con el verbo SER. Y, así, nosotros irónicamente
decimos que predica “el milagro de la transmutación”.
El presente ensayo lo dedicamos a
poner de manifiesto los citados errores y a plantear un método de análisis para
construir e interpretar las citadas fórmulas. Para mejor seguimiento del
presente estudio, lo hemos dividido en dos partes. La segunda parte es algo más
teórica que la primera y aparecen algunos desarrollos matemáticos.
PRIMERA PARTE
En esta primera parte plantearemos y
explicaremos los pasos a seguir para la construcción de las Fórmulas de
Transformación de Lorentz. A estas
fórmulas les llamaremos: “Fórmulas de la
VISION de la Extensión de un evento observada desde una plataforma móvil”, con
objeto de corregir la tergiversada
aceptación entre los verbos: VER y SER.
1.- UNA EXPLICACION QUE APARECE EN UN LIBRO DE A.EINSTEIN
En el libro “Sobre la teoría de la relatividad especial y
general” de Einstein, en su página 32 (Edición “Alianza Editorial”), describe
la forma y utilidad de las fórmulas llamadas de las Transformaciones de
Lorentz, de la siguiente manera:
“Dadas las cantidades
(x,y,z,t) de un suceso respecto a (k), ¿Cuáles son los valores (x`,y`,z´,t´)
del mismo suceso respecto a (k´)?
Las relaciones hay
que elegirlas de tal modo que satisfagan las leyes de propagación de la luz en
el vacío para uno y el mismo rayo de luz (y además para cualquier rayo de luz)
respecto a (K) y (K´)”.
Y prosigue diciendo:
“El problema queda
resuelto por las ecuaciones”.
Fórmula del Espacio
Fórmula del Tiempo
Y, en esta misma página del citado libro, se dibuja el
siguiente sistema de coordenadas (k) y (K).
Figura 1

Más adelante demostraremos que la expresión:
que
aparece en la fórmula del tiempo, se traduce como un tiempo y que con la “fórmula
del espacio” habría suficiente para hacer aplicaciones “teóricas”.
2.- ¿DONDE ENCONTRAMOS ERRORES EN LA EXPLICACION QUE DA A.EINSTEIN EN LAS
FORMULAS DE TRANSFORMACION DE LORENTZ?
El primer error que encontramos en las explicaciones que
da el físico sobre las Fórmulas de las Transformaciones de Lorentz es el
siguiente:
Al preguntar:
¿Cuáles son los valores (x`,y`,z´,t´) del
mismo suceso respecto a (k´)?
Creemos que está
pensando en la “transformación” o sea en “convertir “más que en VER el suceso
desde una plataforma móvil respecto al suceso. Creemos que este es uno de los
errores. Vuelve a caer en el error que ya hemos comentado en anteriores de
nuestros ensayos. Mediante los movimientos relativos confunde el verbo VER con
el verbo SER. De esta forma prepara lo que nosotros hemos llamado “ el milagro de la transmutación”.
Decimos que está pensando en la “transformación”, ya que en el experimento mental de la barra de
medir longitudes, sometido a un movimiento relativo, aplica la formula de la
transformación del espacio y predica el disparate del acortamiento de la referida barra. Este error consiste en creer
en la “transformación” de la materia.
El Segundo error consiste en querer aplicar
las conclusiones sacadas en un experimento mental, a un experimento físico de la
vida real.
Nos
preguntamos si los resultados obtenidos procedentes de un experimento mental
pueden ser aplicables en la vida real.
Creemos
que la respuesta tiene que ser negativa. Precisamente se razona el problema
aplicando un experimento mental por no poder aplicar un experimento físico. Y,
hasta ahora, parece ser que es una quimera pretender construir un experimento
físico que transcriba los resultados de un experimento mental. Todo esto
agravado si en el experimento mental se ha confundido la acción de VER con el
verbo SER
En
el presente ensayo veremos que nos aparecerá la expresión
En
la que (v) es la velocidad de un cuerpo móvil y (c) es la velocidad de la luz.
Aún considerando la (v) una velocidad de las más grandes en nuestro mundo real,
por ejemplo la velocidad de un cohete espacial, su velocidad es tan pequeña
respecto a la de la luz (c) que el cociente que aparece dentro del radicando de
la expresión que hemos escrito sería un valor infinitésimo. Por eso decimos
que, tal como veremos, sería una quimera traspasarla a un experimento físico.
(NOTA: No confundir, como manifiesta A.
Einstein, con que la velocidad límite que se puede alcanzar es la velocidad de
la luz. El lector puede leer el ensayo contenido en nuestro Blog, titulado:
“Teoría de la relatividad. - Es posible que una partícula pueda viajar a una
velocidad más rápida que la luz”. Observará que allí estamos hablando de una partícula
y no de un cuerpo dotado de movimiento).
3.- ¿QUE ENTENDEREMOS POR DIMENSION DE
UN EVENTO?
Entenderemos por dimensión de un evento su duración desde la aparición del
mismo hasta su extinción. Esta duración podemos valorarla en longitud o en
tiempo. A esta dimensión le llamaremos EXTENSION del evento.
4.- NOS PREGUNTAMOS, ¿EN UN
PLANTEAMIENTO TEORICO, PARA QUE SERVIRIAN
LAS FORMULAS DE TRANSFORMACION?
Según nuestro enfoque diremos que su
finalidad sería: Valorar la dimensión de un evento, que acontece en una
determinada posición del espacio, por un observador que se está moviendo a
velocidad (v) constante y rectilínea respecto a este evento.
(NOTA: Observe el lector que hablamos
de un planteamiento “teórico”. Al final expondremos que este planteamiento
utilizando los recursos matemáticos, difícilmente lo podríamos aplicar en
nuestra vida real).
5.- FORMULA DE LA TRANSFORMACION DE
LA VISION DE LA EXTENSION DE UN EVENTO
Para no confundir con la errónea
finalidad que pretende dar Einstein a las fórmulas de transformación de
Lorentz, nosotros en nuestro análisis las llamaremos: Formulas de
transformación de la VISION de la Extensión de un evento. Dese cuenta el lector
que hacemos destacar el verbo VER.
6.- ACCIONES IMPLICITAS EN LA TRANSFORMACION
DE LA VISION DE LA EXTENSION DE UN
EVENTO
Para construir la “formula de la
transformación de la VISION de la Extensión de un evento”, en nuestro estudio
consideraremos tres acciones implícitas en ella. Estas acciones son las siguientes:
APARECER el evento; PERMANECER su visibilidad;
VER su Extensión.
7.- DOS FENOMENOS FISICOS A
CONSIDERAR
En la construcción de la fórmula de
transformación debemos tener en cuenta que se solapan dos fenómenos físicos. Uno
es el movimiento y desplazamiento del observador del evento a una velocidad
(v). El otro fenómeno físico es la VISION del evento, desde el lugar en que se
ha desplazado el observador, y en la que esta implicada la velocidad de la luz
(c).
8.- UN TRIANGULO RECTANGULO PARA ANALIZAR
DESDE UNA PLATAFORMA MOVIL LA VISION DE
LA EXTENSION DE UN EVENTO
Para analizar la VISION de la
Extensión de un evento desde una plataforma móvil nos auxiliaremos de un triángulo
rectángulo.
Hemos de definir la situación de tres
puntos representativos de: Aparición del evento (E); Finalización de la
Extensión del evento (F) y Observación del evento (O). Con estos tres puntos definimos un triángulo.
9.- ¿POR QUE EL TRIANGULO HA DE SER
RECTANGULO?
Para posicionar en el espacio el
evento y la posición de observación del mismo, consideraremos los dos catetos
del triangulo como unos ejes coordenados. Los catetos del triángulo deben ser perpendiculares
entre si. Esto es así ya que:
En el eje horizontal le daremos el
significado como del recorrido del movimiento y la velocidad (v), y en el eje vertical expresaremos la dimensión de la
Extensión del evento.
Sin entrar en expresiones matemáticas
más especializadas, solo decimos que estos dos ejes de referencia deben tener
direcciones distintas ya que implican conceptos diferentes. O sea, deben ser
linealmente independientes. Deben tener la cualidad de independencia.
10.- REPRESENTACION DEL TRIANGULO
RECTANGULO CON LA EXPRESION DE SUS RECORRIDOS ENTRE SUS PUNTOS
La siguiente figura presenta los
citados tres puntos y sus recorridos entre ellos. Este triangulo servirá para
calcular las relaciones que existen entre los recorridos de la luz y el de un
observador móvil del evento.
Figura 2
El punto (E) es en donde ha aparecido
el evento.
El cateto vertical lo interpretamos
como el equivalente al recorrido de la EXTENSION del evento. Lo indicamos como
(c.tp), siendo (c) la velocidad de la luz y llamando (tp)
Tiempo Propio de la Extensión.
Representamos el final de la
Extensión con el punto (F).
El cateto horizontal sirve para indicar el recorrido y dirección de un
cuerpo móvil que se desplaza a velocidad uniforme y rectilínea (v) desde el
punto (F) al punto (O). Podríamos considerar que es el cuerpo del “observador”.
La hipotenusa de este triángulo representa el
recorrido del rayo de luz que tiene que percibir el observador para VER la
aparición y desarrollo del evento. Su tiempo de recorrido lo escribimos como (tr).
11.- ¿POR QUE SITUAMOS LA EXTENSION
SOBRE EL CATETO VERTICAL?
Ya dijimos que los dos catetos debían ser
linealmente independientes. Ahora nos podemos preguntar porque la Extensión del
evento lo ponemos como una longitud sobre el cateto vertical y le llamamos (tp).
La respuesta es que este valor representa el tiempo en que un observador
situado en el punto final (F) estaría contemplando todo el desarrollo de la
Extensión. Y así, de esta manera plasmamos en un croquis un criterio de
valoración de la Extensión.
12.- RELACION ENTRE EL TIEMPO (tp)
DE LA EXTENSION DEL EVENTO Y EL TIEMPO DE DESPLAZAMIENTO (td)
DEL OBSERVADOR
Hemos desarrollado un procedimiento
matemático que nos permite valorar el tiempo (tp) de la EXTENSION en función del Tiempo de
Desplazamiento (td) que requiere el observador del evento para
recorrer el itinerario descrito por los puntos (F-O).
Situando la EXTENSION del evento en
el cateto vertical del triángulo, valorándola como (tp) y, valorando
el tiempo de desplazamiento (td) que existe entre el punto de
observación (O) y el citado cateto vertical, la relación existente entre ellos
la expresamos de la siguiente manera:
La expresión:
es el llamado FACTOR DE LORENTZ, en dónde (c) es la velocidad de la luz y
(v) la velocidad de un cuerpo móvil.
(NOTA: El desarrollo matemático para
llegar a obtener esta ecuación esta en la Segunda Parte del presente ensayo)
13.-
EL FACTOR DE LORENTZ COMO FACTOR DE TRANSFORMACION DEL TIEMPO DE DESPLAZAMIENTO
(Ttd) EN MEDIDA DE LA EXTENSION (tp) DEL EVENTO.
Para
justificar que el Factor de Lorentz permite transformar el valor del Tiempo de desplazamiento (td) sobre
el cateto horizontal del triángulo al
punto de observación (O), en unidades
del Tiempo Propio (tp) del evento, ó sea su EXTENSION, observaremos
la formula dada anteriormente de la que podemos deducir lo siguiente:
Con
lo que podemos afirmar que el Factor de Lorentz equivale a valorar el (td)
en unidades (tp). Es un
factor transformador que permite valorar
desplazamientos realizados a velocidades (v) y transformarlos en velocidades
(c).
14.-
EXPRESION DE LAS DISTANCIAS EN TIEMPOS EMPLEADOS EN RECORRERLAS
El
expresar las distancias en tiempos empleados en recorrerlas nos permitirá
considerar solo una de las formulas de transformación expuestas en el referido
libro de A.Einstein.
Podemos
expresar la distancia entre dos puntos como el TIEMPO empleado en desplazarse entre
estos dos puntos a una determinada velocidad. Esta velocidad puede ser la de
un cuerpo móvil (v) o bien la de la luz (c).
Puesto
que la velocidad de la luz (c) la podemos considerar constante, la podemos
tomar como medida para valorar distancias y medir estas distancias en unidad de
velocidad de la luz (uvl).
En
la siguiente figura podemos observar que la distancia entre el punto de
observación (O) y sus ejes de referencia móviles (K´), que tiene como referencia el observador, la
podemos cuantificar mediante:
(X – v.(td)).
Figura 3
Por
lo que hemos comentado, esta distancia también la podemos expresar en tiempo
transcurrido en recorrerla (T), a una
velocidad (v).
Por
lo que establecemos la equivalencia:
15.-
LA FORMULA DE LA TRANFORMACION DEL ESPACIO DADA POR A.EINSTEIN IMPLICITAMENTE
CONTIENE LA EXPRESION DE LOS DOS FENOMENOS FISICOS QUE HABIAMOS INDICADO
El que la fórmula de
transformación del espacio de A.Einstein, no cumpla con la finalidad que él le
asigna, esto nos quiere decir que su expresión, implícitamente contiene
los dos fenómenos físicos a considerar.
Observemos que el
numerador de la fórmula es:
que tiene en cuenta el fenómeno físico del
desplazamiento. Esto lo podemos comprobar en la anterior Figura 3.
Respecto al denominador
de la citada fórmula planteamos lo siguiente:
Tal como habíamos
expuesto, si
equivale a permitir valorar el (td) en unidades (tp) y como
es equivalente al (td), podemos deducir que:
queda valorado en unidades (tp). O sea, en la Extensión del
suceso.
Quede claro que nos
permite VER la Extensión del evento. NO transformar el evento.
16.-
OTRA FORMULA PARA VALORAR LA VISION DE
LA EXTENSION DE UN EVENTO DESDE UNA PLATAFORMA MOVIL
En el anterior número
hemos visto que la fórmula de la transformación del espacio que nos da A.Einstein, aunque no se ajuste a la finalidad que el propone, si que podríamos
utilizarla con un enfoque teórico para medir la extensión (tp) de un
evento.
Con fines teóricos
también podemos dar otra expresión que
nos permita obtener el (tp) en función del tiempo de desplazamiento (td)
necesario para cubrir la distancia entre los puntos (F) y (O).
Observe
el lector que esta expresión se obtiene haciendo un despeje de variables en la
ecuación expresada en el Punto 12.
17.-
¿POR QUE A LA FORMULA DE LA
TTRANSFORMACION DEL ESPACIO LE LLAMAMOS
FORMULA DE LA TRANSFORMACION DE LA VISION DE LA EXTENSION DE UN EVENTO?
El
nombre de “fórmula de la transformación de la visión de la extensión de un evento” nos ha surgido al
investigar la construcción y posible empleo de esta fórmula. Por lo que el
lector puede llamarla como a él le plazca.
Nosotros
la hemos llamado de esta manera por lo siguiente:
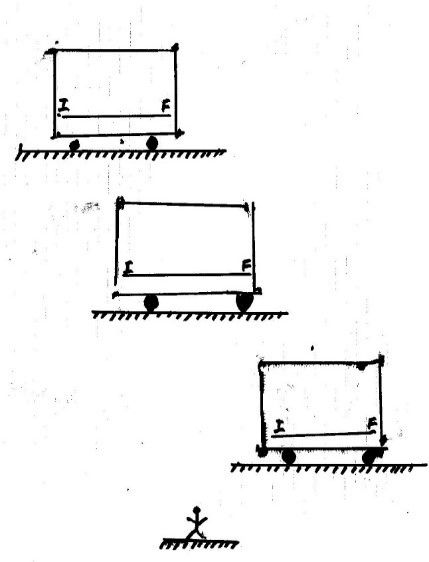
Podemos
hacer una composición de las figuras 1 y 2 sobreponiéndolas una encima de la
otra para que así, globalmente, represente la expresión gráfica de la citada
formula que, según habíamos comentado es la expresión de los dos fenómenos
físicos.
En
la siguiente figura podremos ver que aparecen tanto las variables que implican
el traslado de los ejes coordenados, como las variables relacionadas con la
visión del evento desde un punto de observación móvil. O sea, las variables
correspondientes al triangulo rectángulo.
Figura 4
Si
considerásemos que no exista movimiento y que el observador está fijo en el
punto (O), este observador VERIA la Extensión del evento situado en el eje (K)
y con una dimensión igual a (E – F). Pero, si ahora consideramos que el
observador se va moviendo y sus coordenadas de referencia son (K´), la VISION del referido evento sobre estas
coordenadas tendrá una dimensión: ( e – f). Con lo que podemos decir que la
VISION del evento SE ha TRANSFORMADO. Y esta dimensión de la Extensión es con
la que debe operar el observador,
18.-
¿SE MANTIENE LA RELACION td/tp AL MOVERSE EL SISTEMA DE REFERENCIA MOVIL?
Podría
aparecernos la duda si con este desplazamiento de coordenadas se
mantiene constante la relación:
que nos hace poder medir el valor de la Extensión
del evento. Utilizando la Geometría podemos decir que si, aplicando el Teorema de Tales.
(NOTA:
Ver en la segunda parte del presente estudio la explicación geométrica del Teorema
de Tales)
SEGUNDA PARTE
Esta segunda parte sirve para exponer
los planteamientos matemáticos e ideas que avalan los criterios que se han
empleado en la primera parte, para la construcción de las citadas fórmulas.
1.- CONDICIONES DE VALIDEZ PARA LA VISION DE LA EXTENSION DE UN EVENTO DESDE UN PUNTO DE OBSERVACION MOVIL.
CONDICIONES DE SINCRONIZACION
Observemos la Figura 2. En un
instante dado ocurre que: en el punto (E ) del espacio aparece un evento y en
este mismo instante el posible observador de este evento se encuentra en el
punto (F) del espacio.
A partir de este instante inicial empieza el
recorrido del rayo de luz que transporta la imagen del suceso y el recorrido
del observador que tiene que detectar tal suceso. Llamando (tr) el
tiempo ocupado en el recorrido del rayo y (td) el tiempo del
recorrido del observador, como los dos recorridos deben coincidir en el punto
de observación (O) impondremos como una condición de sincronización:

Esta es la condición que impondremos en los
cálculos que realizaremos seguidamente.
2.-
DEDUCCION MATEMATICA DE LA RELACION ENTRE EL TIEMPO
PROPIO DE LA EXTENSION DEL EVENTO Y EL TIEMPO DE DESPLAZAMIENTO HASTA EL LUGAR DE
OBSERVACION
Para relacionar el Tiempo Propio (tp) de la
Extensión del evento, con el Tiempo de Desplazamiento (td) aplicaremos
el Teorema de Pitágoras al triangulo rectángulo que dimos como referencia.
Exigiendo el cumplimiento
de la Condición de Sincronización:
nos permite hacer la sustitución de (tr) por
(td) con lo que se obtiene:
Agrupando términos se tiene:
Podemos transformar el denominador de la siguiente
forma:
Eliminando (c), da como resultado
3.- DEMOSTRACION DE QUE AL DESPLAZAR LA VISION DE LA EXTENSION SOBRE EL SISTEMA DE REFRENCIA MOVIL SE MANTIENE LA RELACION ENTRE EL (td
) Y EL (tp)
Para demostrar este cumplimiento
debemos recordar el Teorema de Tales. Podemos decir que en un triángulo rectángulo
se cumple la relación de proporcionalidad entre el recorrido del cateto
horizontal y el cateto vertical.
Recordemos
que en el cateto vertical representaremos la Extensión (tp) del
Evento y en el cateto horizontal el tiempo de desplazamiento del observador.
La siguiente figura pretende
demostrar la validez de este teorema, al observar que se mantienen las
referidas proporciones
Figura 5

4.- DEMOSTRACION DE QUE EL SEGUNDO
FACTOR DEL NUMERADOR DE LA FORMULA DEL TIEMPO SE PUEDE TRADUCIR COMO UN TIEMPO
Al exponer la fórmula de la
transformación del tiempo dijimos que la expresión:
no es
mas que la expresión de un “tiempo”.
Vamos a demostrar esta afirmación.
En la VISION de un
evento, en el que empleamos un Sistema de Referencia móvil (SRM) respecto a un
Sistema de Referencia Fijo (SRF), hay que tener en cuenta que utilizamos dos
tipos de velocidades de naturaleza completamente diferente. Recordemos que se
trata de: (v) y (c). Debemos homologar estos dos conceptos si queremos
incorporarlos en la ejecución de un mismo fenómeno físico. Utilizamos la
velocidad de la luz (c) como patrón de medida. O
sea, los 300.000 kms/seg como unidad de
velocidad.
Para hacer las
referidas conversiones debemos tener en cuenta los siguientes criterios a
seguir:
Todas
las longitudes se cuantificarán utilizando: “unidades velocidad luz” (uvl).
Esto
quiere decir que: las (uvl) son las que se consumirían para desplazarse entre
dos determinados puntos de referencia.
Por ejemplo, podemos escribir: x = k (uvl) refiriéndonos a que una
determinada longitud (x) se encuentra, o requeriría k (uvl), para llegar a ella.
Una relación tal como:
(v / c) asigna una fracción de (uvl) a una determinada velocidad (v), ya que
(c) es una cantidad fija que se toma como unidad, mientras que (v) es la
velocidad relativa entre los Sistemas de Referencia Inerciales, valor diferente
en cada caso en concreto.
Para cuantificar una
longitud (l) aplicaremos la expresión:
Esta expresión responde
a la pregunta: Una longitud (x) que se ha recorrido a la velocidad (v) ¿a qué
longitud (l) equivale si la velocidad fuese la de la luz (c)?
Para obtener el tiempo
de desplazamiento (td) de un Sistema de Referencia Móvil (SRM) sobre
el eje (X), operando con (uvl), deberemos dividir el espacio (l) por la
velocidad de la luz (c).
O sea:
y como
se obtiene: